Doppler broadening and Lamb-Dicke regime

Doppler broadening

Doppler broadening can be a problem if you wish to perform precise spectroscopy. For example, consider a clock transition in thulium atoms. Its natural linewidth is ~1 Hz. However, the cloud of atoms which one observe in order to perform spectroscopy of this clock transition has a certain velocity distribution. If a cloud is in a thermalised state it is well described by a Maxwell distribution with a temperature T: $$P_v = \sqrt{\frac{m}{2\pi kT}}\exp{\left(-\frac{mv^2}{2kT}\right)}$$

Each velocity provides Doppler shift $f = f_0(1 + v/c)$, thus transferring the distribution of velocities to the distribution of frequencies: $$P_f = \frac{c}{f_0}P_v\left( c \left( \frac{f}{f_0}-1 \right) \right)$$

$f_0$ here is the center frequency of the transition with wavelength ~1.14 µm. Due to atoms’ thermal movement, their absorption (or emission) spectrum of the clock transition becomes broadened, with full width at half maximum being $$\Delta f_{FWHM} = f_0\sqrt{\frac{8kT\ln{2}}{mc^2}}$$

Laser cooling provides us with the cloud at a temperature of about 10 µK. Mind you, it is rather low (although we are trying to improve). Still, with the mass of 169 atomic units (for $^{169}$Tm) we get $\Delta f_{FWHM}$ = 46 kHz, which is greater than natural linewidth of 1 Hz by quite a bit. What do we do, then?

Spatial confinement

Different applications of optical clocks based on neutral atoms make use of optical lattice for several reasons. Different application of optical clocks based on a single ion use ion trap for obvious reasons. Both confine particles in a sharp close-to-harmonic potential. This potential restricts movement of atoms. Does it influence the Doppler broadening, then? Yes, it should. While it all depends on several parameters, it is safer to take quantum mechanical approach from the beginning. We can always go back to classical case later.

The harmonic potential provides us with a set of wave functions and corresponding energy levels $E_n = \hbar \Omega (n+1/2)$. We have to abide to these energy levels when we write the conservation law for the process of absorbing/emitting a photon: $$\hbar \omega = \Delta E_{internal} + \hbar \Omega \Delta n$$

This simple equation describes absorption/emission of a photon together with any mechanical movements. It must therefore contain Doppler shift, and it must contain recoil energy. Somehow they all should be related to $\Delta n$.

Before going any further, let us keep all the relative equations about quantum harmonic oscillator at hand. I will simply write them down without any explanation: $$H = \frac{p^2}{2m} + \frac{1}{2} m \Omega^2 z^2 \\ z = \sqrt{\frac{\hbar}{2m\Omega}} (a^\dagger + a) \\ p = i\sqrt{\frac{\hbar m \Omega}{2}} (a^\dagger - a) \\ H = \hbar \Omega(a^\dagger a + 1/2) \\ a^\dagger a |n> = n |n>$$

Lamb-Dicke regime

We want to describe the effect of photon absorption/emission on atomic wave function in a harmonic potential. For that purpose we use the displacement operator for the momentum: $\exp (i k z)$. In the basis of vibrational states, we get probability amplitudes $\langle n’| \exp (i k z) |n \rangle$ for a transition $|n\rangle \rightarrow |n’\rangle$. Introducing the following parameter, we get: $$\eta^2 = \frac{\hbar k^2}{2 m \Omega} = \frac{\omega_{recoil}}{\Omega} = \left( \pi \frac{a_0}{\lambda} \right)^2 \\ \exp (i k z) = \exp (-i \eta (a^\dagger + a))$$

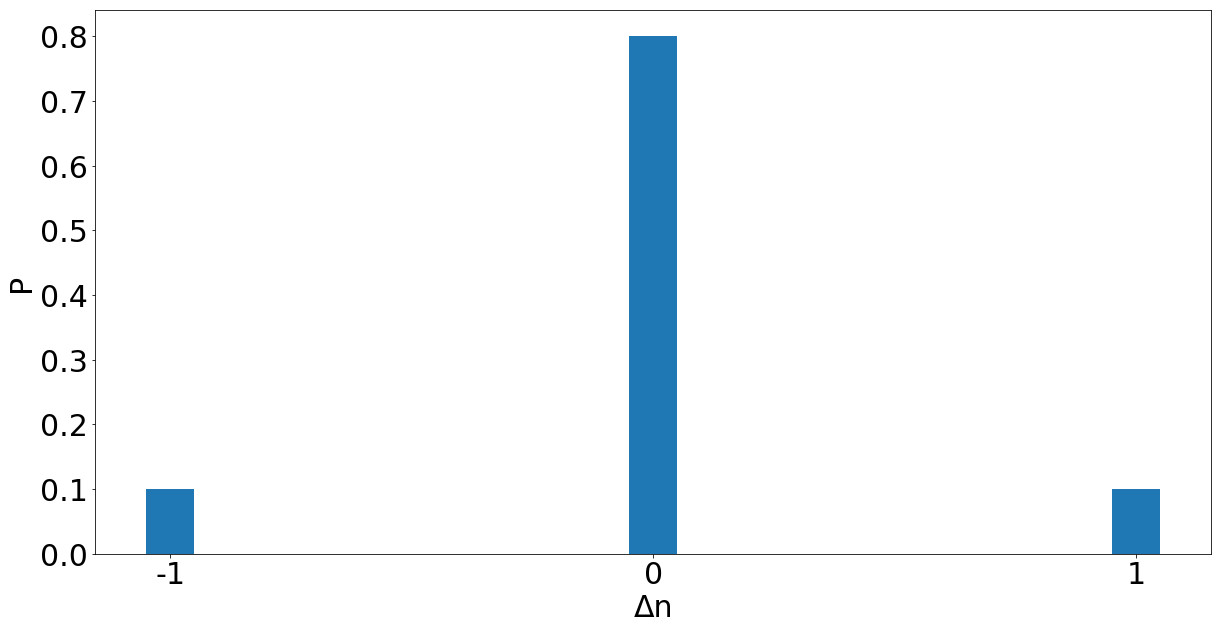
Lamb-Dicke regime is the case of small $\eta\sqrt{n+0.5}$. We can expand the exponent: $$\langle n'| \exp (-i \eta (a^\dagger + a)) |n \rangle = \delta_{n',n} \left( 1-\eta^2(n+1/2) \right) - i \eta \left( \sqrt{n'} \delta_{n',n+1} + \sqrt{n} \delta_{n',n-1} \right)$$

We see that $\Delta n = n’ - n \neq 0$ is very unlikely, and $|\Delta n| > 1$ even more so. Generally atom does not change its state in the harmonic potential while emitting/absorbing photon. And according to $\hbar \omega = \Delta E_{internal} + \hbar \Omega \Delta n$ we are unlikely to witness the influence of any motional phenomena, i.e. Doppler shift or recoil.

This is very much like the Mössbauer effect (phononless nuclear resonance). Only instead of a solid that bounds atomic nuclei, here we have our huge setup that gets all the recoil momentum from the photon.

Doppler broadening again

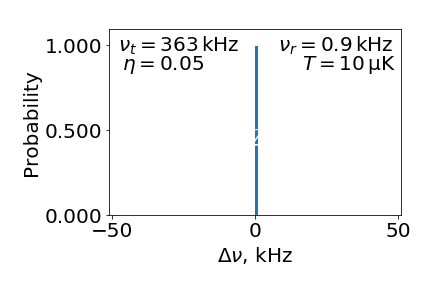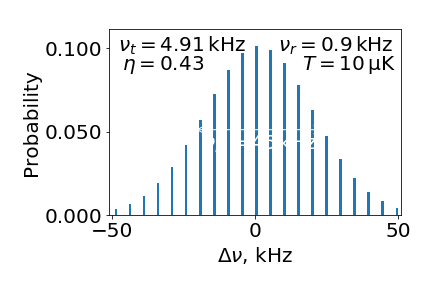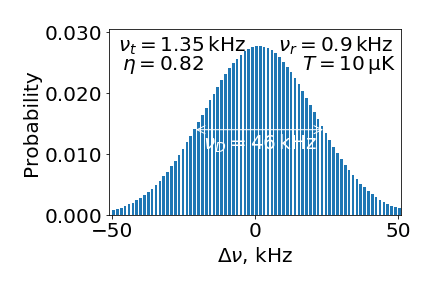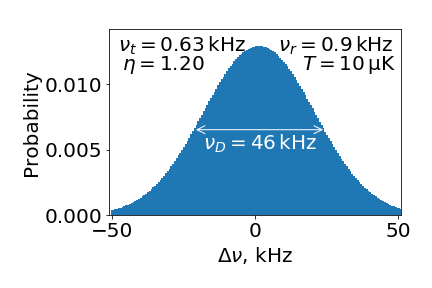
If we want to get back to the classical picture, for large $n$ the matrix element mentioned above becomes Bessel function: $$\left| \langle n+\Delta n| \exp (-i \eta (a^\dagger + a)) |n \rangle \right| = \left| J_{\Delta n} \left( 2 \eta \sqrt{n} \right) \right|$$

which peaks as a function of $\Delta n$ near $2 \eta \sqrt{n}$. $\Delta n$ gives us the frequency shift, and $\sqrt{n}$ proportional to velocity. Thus we come back to the Doppler shift, and after considering thermal distribution of velocities - to the Doppler broadening. You can see the transformation to classical picture below. Here $\nu_t = \Omega/2\pi$, $\nu_r = \omega_{recoil}/2\pi$ and $T$ is temperature of the atomic ensemble.

Reference

This post was mainly inspired by the lecture by Wolfgang Ketterle and this work.